Reinforcement Learning

Greg Grudic, Lyle Ungar, Vijay Kumar

Traditional instantiations of RL algorithms appear incompatible with robotics: successful RL implementations are typically characterized by a) small discrete state spaces, b) hundreds of thousands of learning runs are used, and c) exploration is done using stochastic search. In comparison, robot control is characterized by a) large, noisy continuous state spaces, b) only limited learning runs are possible, and c) random  actions can result in dangerous or expensive outcomes. We are currently developing new RL algorithms that are specifically intended for large  continuous state spaces of the types typically found in robotics. 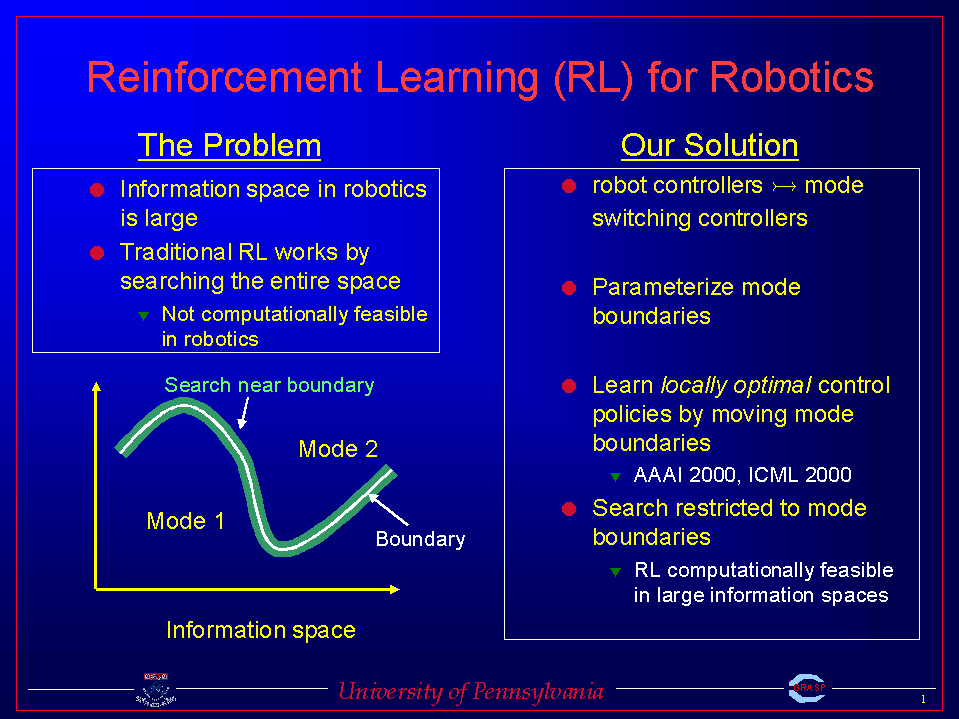Our first results include 1) Boundary Localized Reinforcement Learning (BLRL) and 2) Action Transition Policy Gradient (ATPG). BLRL develops a policy gradient framework for mode switching in high dimensional state spaces, and shows that search can be made computationally tractable even in very high dimensional state spaces through the use of deterministic modes.   Finally, BLRL shows the locally optimal mode switching policies can by found by restricting search to near mode boundaries.

ATPG is a policy gradient algorithm that is theoretically guaranteed to find locally optimal policies and can be applied to both deterministic mode switching controllers and stochastic controllers. By restricting policy gradients (PG) estimates to when relative estimates of the value of executing actions is available (which in continuous state spaces corresponds to when the agent changes actions), ATPG converges orders of magnitude faster than traditional PG algorithms such as REINFORCE, as well as newer algorithms which use function approximation techniques to improve convergence.