Catching Plagiarists
This homework presents a real problem that requires a software solution. Your goal is to try to quickly determine the similarities between documents in a large set to see if you can detect plagiarism.
Topics: File I/O, Java Collections, Iterators, Algorithm Efficiency, Testing
Due Date: February 12 @ 11:59PM
Starter Files Here & README Template Here
Background
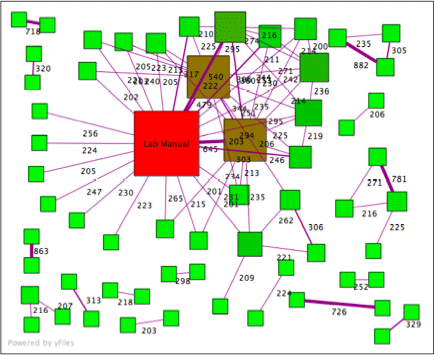
Below is an actual graph of lab reports submitted for an introductory Physics course at a large university. This graph represents a portion of data collected for about 800 lab reports. In the graph, each node represents a lab report and each edge indicates the number of 6-word phrases shared between two documents. To reduce visual clutter, a threshold of 200 common phrases has been set, so a document sharing fewer than 200 6-word phrases with all other documents is not shown. The “Lab Manual” is a style-guide for the lab report and the two brown boxes are sample lab reports that were distributed; as you can see, many students apparently “borrowed liberally” from these help materials. Particularly suspicious are clusters like the one in the top-right corner: those documents have an inordinate number of 6-word phrases in common with each other. It is likely those people turned in essentially the same lab report or copied large portions from each other.
In order to detect likely cases of plagiarism, you will find the common word sequences among a closed set of documents. Your input will be a set of plain-text documents and a number n; your output will be a representation showing the number of sequences of n words (called n-grams) that each document has in common with every other document in the set. Using this representation, you will identify suspicious groups of documents that share many common n-grams among themselves but not with others.
Output
We could first think of our intended output as a \(D \times D\) matrix, where \(D\) is the total number of documents. Each cell of the matrix will represent the number of shared n-grams between the corresponding pair of documents:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | - | 4 | 50 | 700 | 0 |
| B | - | - | 0 | 0 | 5 |
| C | - | - | - | 50 | 0 |
| D | - | - | - | - | 0 |
| E | - | - | - | - | - |
From this table, we can conclude that the writers of documents A, C and D share a high number of similar 6-word phrases. We can be fairly certain that A and D collaborated on this assignment. However, printing and storing a \(D \times D\) matrix is unmanageable for large sets: look at how many wasted spaces we have for \(D = 5\)! You should instead produce a list of documents ordered by number of “hits”. For example:
700: A, D
50: A, C
50: C, D
5: B, E
4: A, B
We’ve gone from 25 entries to 5 without losing any information! For even larger sets of documents, it may be important to only report document pairs with a high number of shared n-grams above a certain threshold.
The Documents
We will provide you with different folders of documents that represent the sets. One set will be small (~25 documents); its size will allow you to calculate expected values for unit tests using this set. The other sets will be larger: one has 75 documents and the other has over 1300 documents (the documents came from www.freeessays.cc, a repository of really bad high school and middle school essays on a variety of topics).
Strategy Discussion
For this discussion, we’ll assume that we have \(w\) distinct n-grams across all of our documents. The straightforward matrix solution, requiring us to compare each n-gram in a document to all other n-grams in all other documents, has an \(O(w^2)\) time complexity. This is polynomial time: fast in some contexts, but the growth will be prohibitive here. For example, if the 25 document set takes 10 seconds to process, the 1300 document set will take several minutes—provided that you can store the matrix representation in memory!
We’ll need to improve on this initial strategy in terms of both time and space complexity. The use of hash tables will allow us to speed up the computation dramatically, but for large numbers of documents, we’ll still run out of program memory. Our solution will be to create supplementary data files that we can store on/load from the disk as needed.
Assignment Steps
Part 0: Read and Understand the Requirements
Understanding the problem is the first step to solving it. Take time to read through this writeup and the provided interfaces/files completely before starting. Make sure you fully understand the assignment before you try to code anything.
Testing is an essential part of every coding assignment and we expect you to test your code thoroughly. You are only required to test the DocumentsProcessor.java file for this assignment. To receive full credit, 80% code coverage must be obtained. Name your testing file DocumentsProcessorTest.java. Failure to submit a test class with this name that compiles will result in a grade of zero for the assignment.
Upon unzipping the starter files (hw1-plagiarist-students.zip), you should see 3 classes (DocumentIterator.java, Similarities.java, and Tuple.java), 1 interface that you will be implementing in its own class (IDocumentsProcessor.java), and 3 document sets (big_doc_set, med_doc_set, and sm_doc_set). Each part of this homework will detail the files and methods you will need to implement. Do not modify any of the method headers detailed in the classes and interfaces, as this will cause the autograder to fail!
Part 1: Processing the Documents
Files:
DocumentIterator.java,DocumentsProcessor.java
For this part, you will first modify the provided DocumentIterator.java and then use it to implement the method processDocuments(), defined in the IDocumentsProcessor.java interface.
We require that you use an Iterator to iterate through the contents of each of the text documents to identify the n-grams. To do this, modify the DocumentIterator.java constructor so that it takes in a Reader and a value n in that order. Then, modify the next() method so that it yields an n-gram. You should ignore non-letter character and convert all Strings to lowercase. As provided, the DocumentIterator.java gives you a model of how to iterate over the 1-grams of a document.
You may be tempted to use the Reader’s mark() and reset() to read the n-grams, but we advise you not to use this method. Instead, you should use an array as a buffer for the previous (n-1)-gram instead.
Understanding n-grams
Suppose, for example a document contains the sentence
“This hw is about catching plagiarists”and we choosen = 4. To save space, we should eliminate concatenate the words in each n-gram. The appropriate n-grams would be:
["thishwisabout", "hwisaboutcatching", "isaboutcatchingplagiarists"]
The function processDocuments() processes a set of documents in a director using your DocumentIterator. The directoryPath input represents the path to the respective directory of files, and n represents the number of words in our n-grams. The Map (output) associates each document (its name) to a list containing its n-grams.
Example for
processDocuments()if a folder/directory “test_files” contains two text files:
file1.txt: “This is a file.”
file2.txt: “This is another file.”Calling
processDocuments("test_files", 2)should return a Map with contents:
{"file1.txt"=["thisis", "isa", "afile"], "file2.txt"=["thisis", "isanother", "anotherfile"]}
Checkpoint 1:
Analyze the space and time complexity of the next() and processDocuments() methods that you just wrote. Write your analysis in your README.txt file.
Part 2: Storing the N-Grams
Files:
DocumentsProcessor.java
Now, implement the storeNGrams() method. Your solution will be an example of indexing, which is a clever way of storing and retrieving data on demand based on the size of each document in the file. We will return to indexing later on in the course.
This method should create a single file at ngramFilePath containing all of the n-grams across all of the documents into that file. Separate the n-grams with spaces. You have access to the n-grams from the input Map docs, which is the output of the processDocuments() method. In addition to writing to this file (yay, side effects!), you will also return a List of Tuple objects, each associating the name of the document to its size in bytes. Don’t forget to include the added spaces in the size calculation.
Example for
storeNGrams()if a folder “test_files” contains two text files:
file1.txt: "This is a test document."
file2.txt: "This is also a test document."Calling
storeNGrams(docs, 4)should return aListwith contents:
[("file1.txt", 28), ("file2.txt", 42)]We can confirm that each of the file sizes are correct by forming the n-grams of the file and counting the subsequent bytes of each n-gram. For instance, file1.txt produces the following 4-grams (n=4):
[“thisisatest”, “isatestdocument”]If we count the total number of bytes contained in each 4-gram here, we get 11 and 15, totalling up to 26. We must also account for the spaces written after each n-gram in the written file, which would add 2 more bytes, thus totalling 28. You may try this process as well for file2.txt.
Checkpoint 2:
Analyze the space and time complexity of the storeNGrams() method that you just wrote. Write your analysis in your README.txt file.
Part 3: Similarity Objects and Computing Similarities
Files:
DocumentsProcessor.java,Similarities.java
The Similarities object encapsulates two documents (identified by their filenames) and a count of the n-grams they have in common. So that we can determine which pairs of documents are the most similar, we have that Similarities implements Comparable<Similarities>. This means that you will need to implement the compareTo() method for Similarities. Think: which field(s) should you use to compare two Similarities?
Document Names in Similarities
When comparing two files, their order in the fields of Similarities should have a consistent order, where the file1 is the document with the name that is earlier alphabetically.
For instance, if we encounter a match between
doc_b.txtanddoc_a.txt, in either order (doc_a.txtfirst,doc_b.txtsecond, ordoc_b.txtfirst,doc_a.txtsecond), the Similarity formed between these files should have the exact following fields:
file1 = "doc_a.txt"andfile2 = "doc_b.txt"
Next, implement computeSimilarities(): this method will take the file path of the n-gram file and the index list (both created by storeNGrams()) as inputs and return a TreeSet<Similarities>. When creating this TreeSet, make sure that you traverse the n-gram file just once: this will help you avoid exponential runtimes and losing points!
Why TreeSets?
The
TreeSetdata structure is ordered, making it convenient to find the most similar document pairs in the completed structure. Inserting into aTreeSetis a bit slower than inserting into aHashSet, but there is a significant speedup when trying to find the top/bottom values in the Tree implementation. ATreeSetrequires that its entries implement theComparableinterface in order to make this possible.
Here is a broad outline for how to build your TreeSet:
- If an n-gram is found in two documents and the corresponding
Similaritiesobject is not yet in the set, create that object and then add it to the set. - Otherwise, if those two documents already had a corresponding
Similaritiesobject in the set, then find it and increment its count. You will find thefloor()method in theTreeSetclass will be very helpful for finding particular items in your TreeSet.
This will help you to build an exhaustive TreeSet, where any pair of documents with at least one n-gram in common is present in the Set but no pair is present more than once.
You might find it necessary to use additional data structures when implementing computeSimilarities(). These data structures should be kept local (not stored as instance variables) and you should be mindful of the runtimes of the operations for the structures that you choose.
Example for
computeSimilarities()If a folder “test_files” contains three text files:
test1.txt: "No one can copy from me. You can try if you want to"
test2.txt: "One can copy from me. I will try to copy others."
test3.txt: "To copy others is my hobby. I can copy from anyone. You want to can copy from me as well?"Calling
computeSimilarities()based on trigrams should return aTreeSetcontaining three Similarities objects:
[{file1="test2.txt", file2="test3.txt", count=3},{file1="test1.txt", file2="test3.txt", count=3},{file1="test1.txt", file2="test2.txt", count=3}]
Checkpoint 3:
Analyze the space and time complexity of the computeSimilarities() method that you just wrote. If you use any data structures in this method, make sure to detail how their functions contribute to the complexities as well. Write your analysis in your README.txt file.
Part 4: Print Similarities
Files:
DocumentsProcessor.java,Similarities.java
Next, implement the printSimilarities() method, which takes the TreeSet of Similarities objects returned by computeSimilarities() and a similarity threshold number and prints all pairs of documents that have a number of shared n-grams exceeding the threshold. Print this list of document pairs in descending order; in order to do this, you may need to create a new Comparator<Similarities> in order to do so.
You can review Comparators here.
Checkpoint 4:
Analyze the space and time complexity of the printSimilarities() method that you just wrote. Write your analysis in your README.txt file.
Part 5: Improved Performance
The approach that we’ve outlined in Parts 0-4 already solves our problem: given a set of documents, we can find all of the document pairs that have the most overlap. There is a problem, though: this approach requires us to store a Map in program memory containing all n-grams in all of the documents. For a large document set, this will not be feasible!
We will refactor our code by merging the processDocuments() and storeNGrams() methods. This new method, called processAndStore(), has the following signature:
List<Tuple<String, Integer>> processAndStore(String directoryPath,
String sequenceFile,
int n);
This method will take the path to the document folder, the path to the output file, and the size of the n-grams as input. You will not create a Map containing all n-grams; instead, you will store all the n-grams directly into the n-grams file, reducing demands on program memory (RAM) dramatically. This method will return the List of tuples of files and their sizes in the sequence file.
Checkpoint 5:
Analyze the space and time complexity of the processAndStore() method that you just wrote. Compare this complexity to the original two methods. How does this implementation improve upon using the original 2 methods? Write your analysis in your README.txt file.
Part 6: Submit to Gradescope
Submit all of your classes (DocumentIterator.java, DocumentsProcessor.java, DocumentsProcessorTest.java, Similarities.java, Tuple.java), the README.txt file containing your written analyses, and all relevant testing files to Gradescope.
Submitting testing files
To submit any directories that you build for your own test cases, make sure to read the following carefully. First, place these directories directly in the same place that your source code lives. Second, make sure that the directories use relative paths (e.g.
my_testsinstead of/Users/sharry/Documents/hw1/my_tests). Finally, when you go to submit, please zip each of the directories up independently. Ask in OH if you need help with this.
Make sure that you follow all of the CIT 5940 testing guidelines so that the autograder runs properly on your submission. Submissions without a test class will result in a grade of zero on the assignment.
- Achieve high code coverage
- Write unit tests for everything
- Prefer many unit tests with just one or two assertions
- Some longer tests with many assertions may be appropriate, but these aren’t as useful for debugging
- Submit all files required for testing, including any text or data files you may have generated.
Don’t forget to polish, comment, and take pride in your code! You worked hard to finish this assignment, so make sure that the presentation of your code reflects that.
Style Checking Here is a link to instructions for installing an automated style checker for Eclipse and for IntelliJ. This style checker uses exactly the same guidelines that you’ll be graded on; that is, if you pass these style checks in your IDE, you’ll get full credit on the style portion of your grade!
Grading
Your grade will consist of points you earn for submitting the homework on time and for the final product you submit.
The assignment is worth 220 points.
| Description | Points |
|---|---|
| DocumentsIterator | 15 |
| ProcessDocuments | 27 |
| Storing n-grams on disk | 27 |
| computeSimilarities | 27 |
| printSimilarities | 15 |
| Performance | 24 |
| Commenting, Documentation, and Style | 15 |
| Testing | 50 |
| Readme | 20 |
Testing is worth a lot of points! Here are a few additional guidelines:
- All test cases must contain an assertion. There will be a flat 10 point penalty if any test is missing an assertion statement.
- All of your tests must pass. Remove failing tests. There will be a flat 10 point penalty if any test fails.
- You will earn full credit for meeting the previous two criteria and achieving at least 80% code coverage.
This assignment was originally developed by Baker Franke and was adapted for Penn by Eric Fouh. This version of the assignment was updated by Harry Smith and Voravich Silapachairueng, 2025.